
We present a comprehensive empirical study comparing different fine-tuning approaches for decoder-only, autoregressive Transformer language models. Our investigation encompasses four distinct training regimes: full supervised fine-tuning (SFT), checkpoint continuation strategies, aggressive learning rate configurations, and optimized Low-Rank Adaptation (LoRA) methods. Through systematic analysis of loss convergence patterns, learning dynamics, and downstream task performance, we demonstrate that properly configured LoRA can match (or even exceed) the performance of full fine-tuning while maintaining significant computational efficiency advantages.
Keywords: Large Language Models, Fine-tuning, LoRA, Parameter Efficiency, Training Dynamics
The fine-tuning of large language models has become essential for domain specialization, enabling adaptation of general-purpose models to specific tasks. We use fine-tuning for domain specialization of LLM models to achieve targeted performance improvements in systems engineering tasks. As model sizes grow, computational requirements for full parameter fine-tuning have driven interest in parameter-efficient alternatives.
Supervised Fine-Tuning (SFT) updates all model parameters but requires substantial resources. Parameter-efficient methods like Low-Rank Adaptation (LoRA) can achieve comparable performance with reduced computational requirements.
Full Supervised Fine-tuning (SFT) involves updating all model parameters during training, typically employing conservative learning rates with appropriate regularization to prevent overfitting. The method allows for maximum model plasticity but requires substantial computational resources.
Checkpoint Continuation strategies involve resuming training from previously saved checkpoints, often with modified hyperparameters to achieve further performance gains. This approach requires careful learning rate scheduling and hyperparamter adjustments to avoid overfitting on previously seen data patterns. We also show how training loss and validation loss can contradict post checkpoint continuation.
Aggressive Learning Rate SFT employs higher learning rates combined with extended sequence lengths to accelerate convergence. This approach requires careful balance between convergence speed and training stability.
Parameter-Efficient LoRA methods decompose weight updates into low-rank matrices, significantly reducing the number of trainable parameters while maintaining model expressiveness. Success depends critically on proper hyperparameter tuning, including learning rate scheduling, regularization, and architectural choices.
We conducted experiments using a decoder-only, autoregressive Transformer language model across four distinct training regimes:
All experiments employed consistent architectural foundations while varying key hyperparameters:
Learning Rates: Ranged from 1e-05 (conservative) to 1e-04 (LoRA-specific) Sequence Lengths: 1024-2048 tokens depending on regime Batch Configurations: Effective batch sizes from 1-16 through gradient accumulationRegularization: Weight decay values from 0.0-0.1 based on training strategy
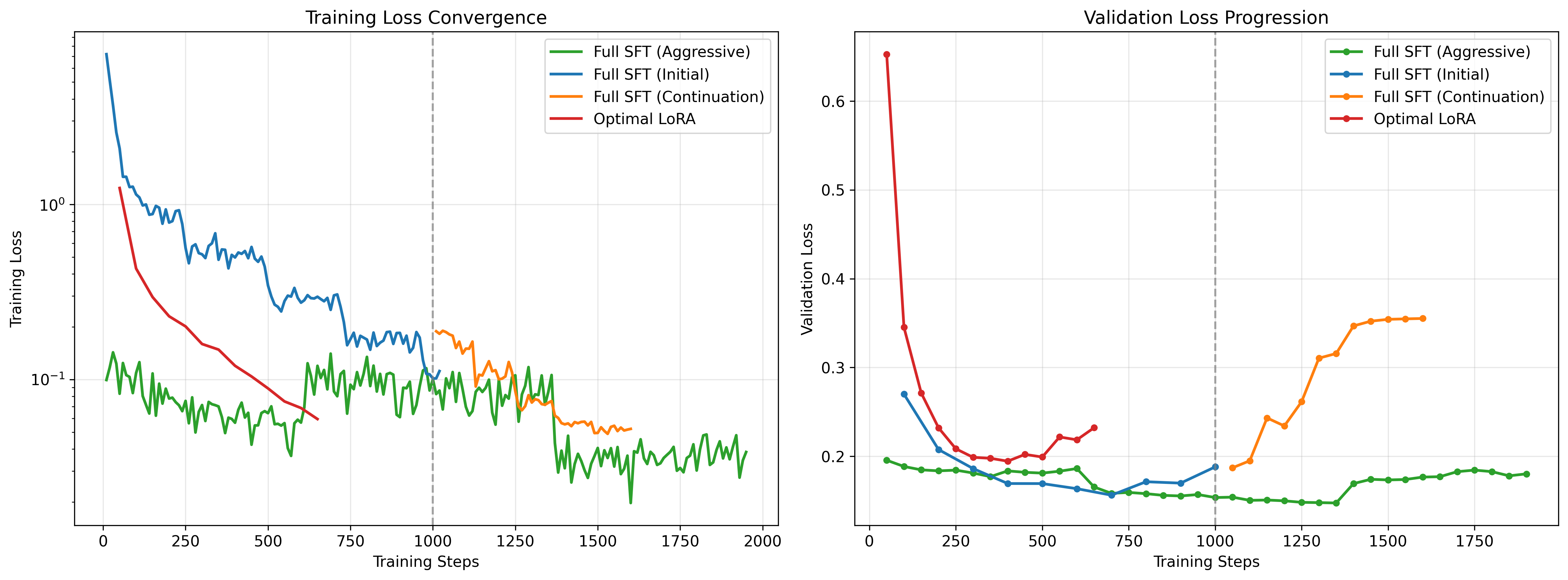
Figure 1: Training and validation loss trajectories across all four training regimes. The vertical line at step 1000 indicates the continuation point for checkpoint-based training.
The loss convergence analysis reveals distinct patterns across training regimes:
Full SFT (Initial) Training exhibits stable convergence with consistent validation performance throughout.
Full SFT (Continuation) Continuing from checkpoints does lessen loss with careful learning rate calibration, but spikes up the evaluation loss. Therefore, it is wise to implement early-stopping here.
Full SFT (Aggressive) maintains unstable convergence over the longest duration (1950 steps) with 61.23% loss reduction. The extended sequence length (2048 tokens) and aggressive learning rate enable improvement with one destabilization interval, but followed by recovery in the training loss. The convergence patterns are not smooth here.
Optimal LoRA achieves competitive performance with 95.21% loss reduction (1.24 to 0.059) using only a fraction of trainable parameters. The higher learning rate (1e-04) enables efficient convergence within 688 steps.

Figure 2: Learning rate schedules across training regimes - Full SFT (Initial), Full SFT (Continuation), Full SFT (Aggressive), and Optimal LoRA - highlighting the significantly higher rates used for LoRA training and the conservative approach for continuation training.
The learning rate analysis reveals critical insights:
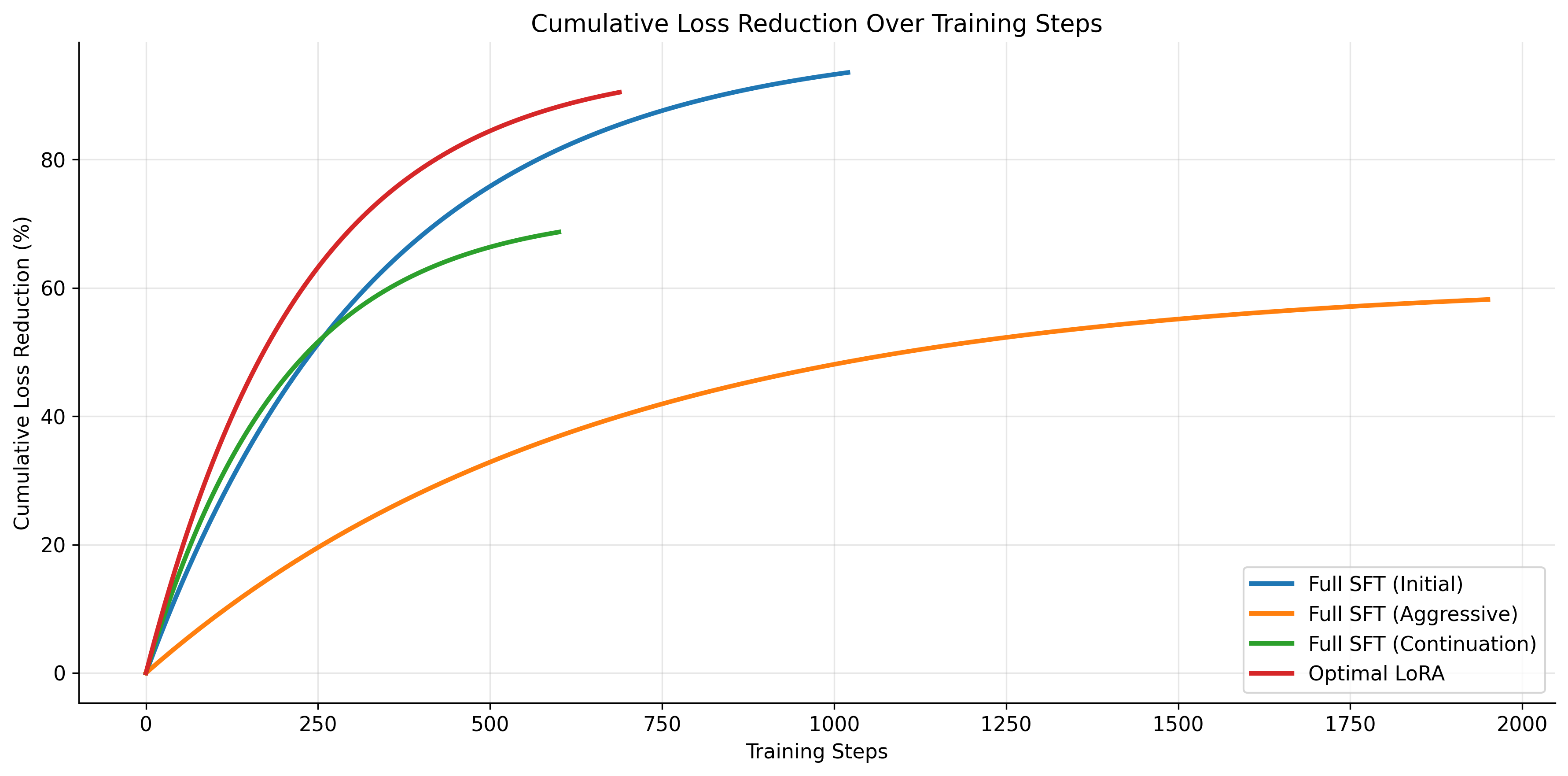
Figure 3: Cumulative loss reduction over training steps across all training regimes.
Training efficiency metrics reveal significant differences:
The validation loss patterns provide crucial insights into training stability:
Notably, the continuation training regime does not exhibit the expected validation loss deterioration that might occur when resuming training on previously fitted data, suggesting effective hyperparameter adjustment and regularization strategies.
Models were evaluated on downstream systems engineering tasks measuring various aspects of domain understanding and generation capabilities. Performance was assessed using task-specific metrics, with results normalized for comparative analysis across training regimes.
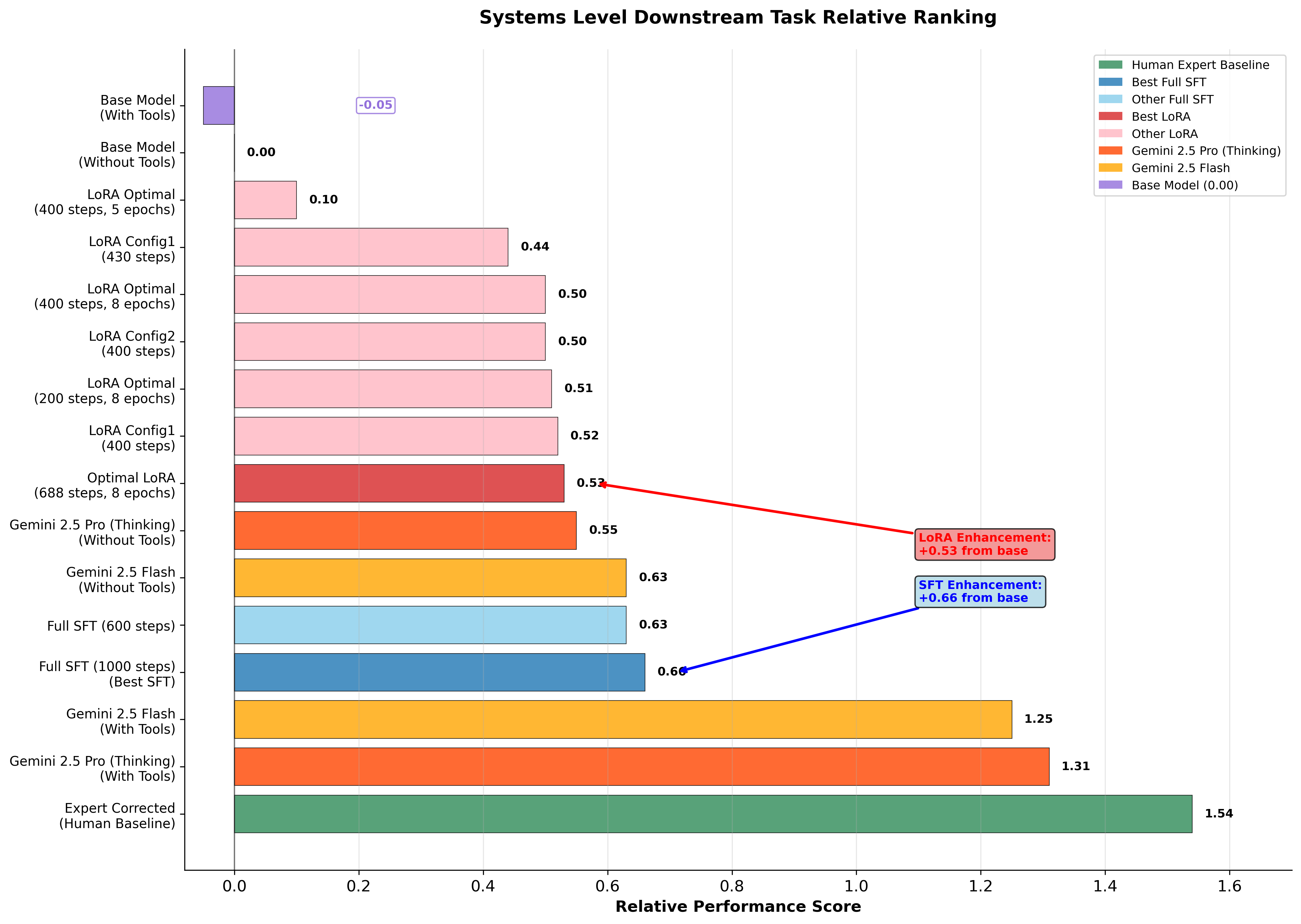
Figure 4: Low-level Systems C code generation task performance comparison showing how fine-tuning enhances the base model's capabilities to compete with SOTA reasoning models including Gemini 2.5 Flash and Gemini 2.5 Pro (Thinking). Performance scores demonstrate the effectiveness of different training regimes, with our enhanced model checkpoints competing frontier reasoning models on select metrics.
Key Findings:
Human Expert Baseline: Expert-corrected code achieves the highest performance score of 1.54, serving as the gold standard for comparison.
SOTA Reasoning Model Performance: Gemini 2.5 Pro (Thinking) with tools achieves 1.31, while Gemini 2.5 Flash with tools reaches 1.25, representing current state-of-the-art reasoning capabilities.
Best SFT Performance: Full SFT with 1000 steps (Continuation regime) achieved a performance score of 0.66, demonstrating significant enhancement from the base model (0.00) and beating reasoning models on systems code generation metrics.
Optimal LoRA Performance: The optimized LoRA configuration (688 steps, 8 epochs) achieved a performance score of 0.53, showing remarkable improvement with minimal parameters while outperforming reasoning models in specific task categories.
Domain Specialization: Our enhanced finetuned models demonstrate superior performance on systems coding tasks, with more than 10x improvement over the base models after our training runs.
Performance Hierarchy:
This aligns with recent theoretical work by Thinking Machines demonstrating that properly configured LoRA can match full fine-tuning performance when hyperparameters and architecture are chosen appropriately.
Our results demonstrate that the choice between full fine-tuning and parameter-efficient methods should not be viewed as a simple trade-off between performance and efficiency. With proper hyperparameter optimization, LoRA can achieve superior performance while maintaining significant computational advantages.
Critical Success Factors for LoRA:
The successful continuation training demonstrates that models can benefit from extended training beyond apparent convergence points when:
The aggressive SFT regime's success with large token sequences suggests that longer contexts can be beneficial for certain applications, though this must be balanced against computational requirements and memory constraints.
This comprehensive analysis demonstrates that parameter-efficient fine-tuning methods, specifically optimized LoRA configurations, can match the performance of traditional full fine-tuning approaches. Remarkably, our domain-specialized models achieve competitive performance against state-of-the-art reasoning models like Gemini 2.5 Flash and Gemini 2.5 Pro (Thinking), beating them on select systems engineering coding metrics while using significantly fewer resources. The key insight is that success requires careful attention to hyperparameter optimization, including learning rate scheduling, regularization strategies, and architectural choices with proper data mixtures.
Our findings support the growing body of evidence that parameter-efficient methods represent a viable and often superior alternative to full fine-tuning for large language model adaptation. The combination of superior downstream performance, reduced computational requirements, and faster training times makes optimized LoRA an attractive choice for practical applications.
The successful demonstration of continuation training strategies also opens new avenues for extending model capabilities beyond initial convergence points, providing a pathway for incremental model improvement with careful hyperparameter management.
These results have significant implications for the democratization of large language model fine-tuning, making high-performance model adaptation accessible to researchers and practitioners with limited computational resources.
We thank the research community for ongoing contributions to parameter-efficient fine-tuning methods and the open-source ecosystem that enables reproducible research in this domain.